【深度学习笔记】误差反向传播（2）

本来打算一天一篇更新，但无奈最近身体有点不适，又鸽了几天。
在【深度学习笔记】误差反向传播（1）中，我们了解了一些误差反向传播的知识，现在，我们就可以把理论转化成代码，去设计实现一个带有反向传播的神经网络，接下来我们一起实现一下反向传播。

还是以上篇文章那些栗子为例（栗子都举起来了，总得吃下去吧）。

加法层和乘法层

上篇文章举的“法外狂徒”张三买手机的栗子中，用到了加法和乘法，那我们就先来实现加法和乘法的反向传播吧，虽然神经网络中用不到，但可以帮助我们进一步理解反向传播的计算图。

加法层

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y
        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy

其中，forward()为前向传播，很简单，就是两个值加到一起，backward()是反向传播，也不难理解，参数 dx、dy 分别是对$x$、$y$的导数，如果理解的不是很清晰的话，不妨看看上一篇文章的公式，结合公式求导去理解。

乘法层

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y
        return out

    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x
        return dx, dy

同样，forward()是前向传播，因为在反向传播的时候要用到前向传播的数据，所以在__init__()函数中定义两个类变量，在前向传播中将输入$x$、$y$保存下来。在反向传播backward()中，对$x$的导数dx就等于反向传播的上一级输入dout乘前向传播的$y$。不知道看到这里有没有疑问，为什么这样就是对$x$的导数呢？想想多元函数偏导数怎么求就很好理解了，对$x$求导，$x$看做变量，$y$看作常数，比如$xy$对$x$求偏导就是$y$。

神经网络中各层的反向传播实现

激活函数层

激活函数我们一共提到过两个比较常用的——ReLU和Sigmoid，我们回顾一下它俩的公式，然后用代码实现一下带有反向传播的版本。

ReLU函数：

$$ y=\begin{cases} x & \text{ if } x>0 \\ 0 & \text{ if } x\leqslant 0 \end{cases} $$

对其求导：

$$ \frac{\partial y}{\partial x}=\begin{cases} 1 & \text{ if } x>0 \\ 0 & \text{ if } x\leqslant 0 \end{cases} $$

代码实现：

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

其中mask是由$True/False$构成的NumPy数组，它会把正向传播时的输入$x$的元素中小于等于0的地方保存为$True$，大于0的保存为$False$。

Sigmoid函数：

$$ y=\frac{1}{1+e^{-x}} $$

很明显，这个函数是一个复合函数，那么我们不急着求导，先把它的每一步计算尽可能拆开，画出计算图看一下：

相比之前画的计算图，Sigmoid函数的计算图除了加法、乘法，还多出了自然指数、除法，我们对各层分别求导没最终得到如下计算图：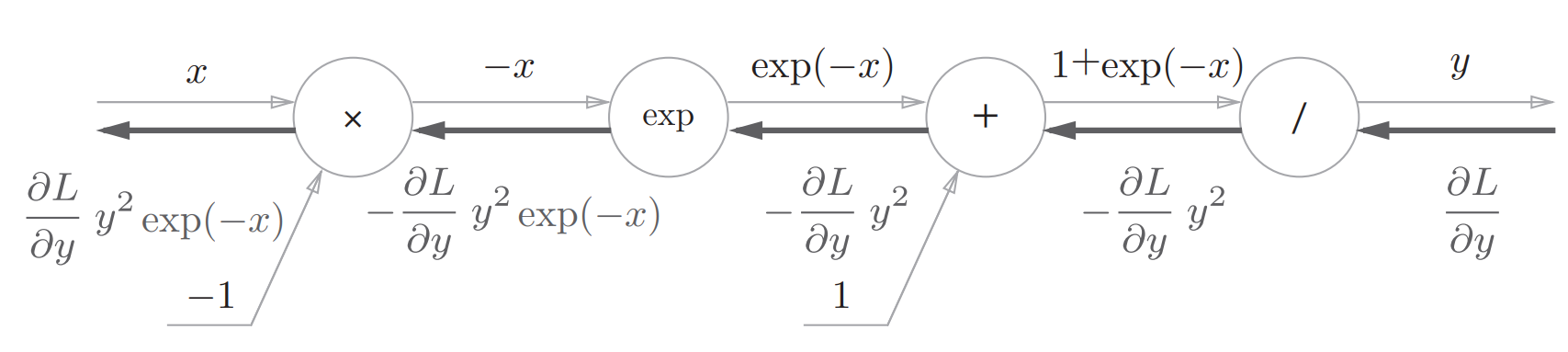

我们对最终反向传播的结果进行整理：

$$ \frac{\partial L}{\partial y}y^2e^{-x}=\frac{\partial L}{\partial y}\frac{1}{(1+e^{-x})^2}e^{-x} \\ =\frac{\partial L}{\partial y}\frac{1}{1+e^{-x}} \frac{e^{-x}}{1+e^{-x}} \\ =\frac{\partial L}{\partial y}y(1-y) $$

根据最后整理的结果，我们来实现一下代码：

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx

Affine层

层如其名，Affine层就是做矩阵变换的层，也就是神经网络的中间各层，其计算图如下：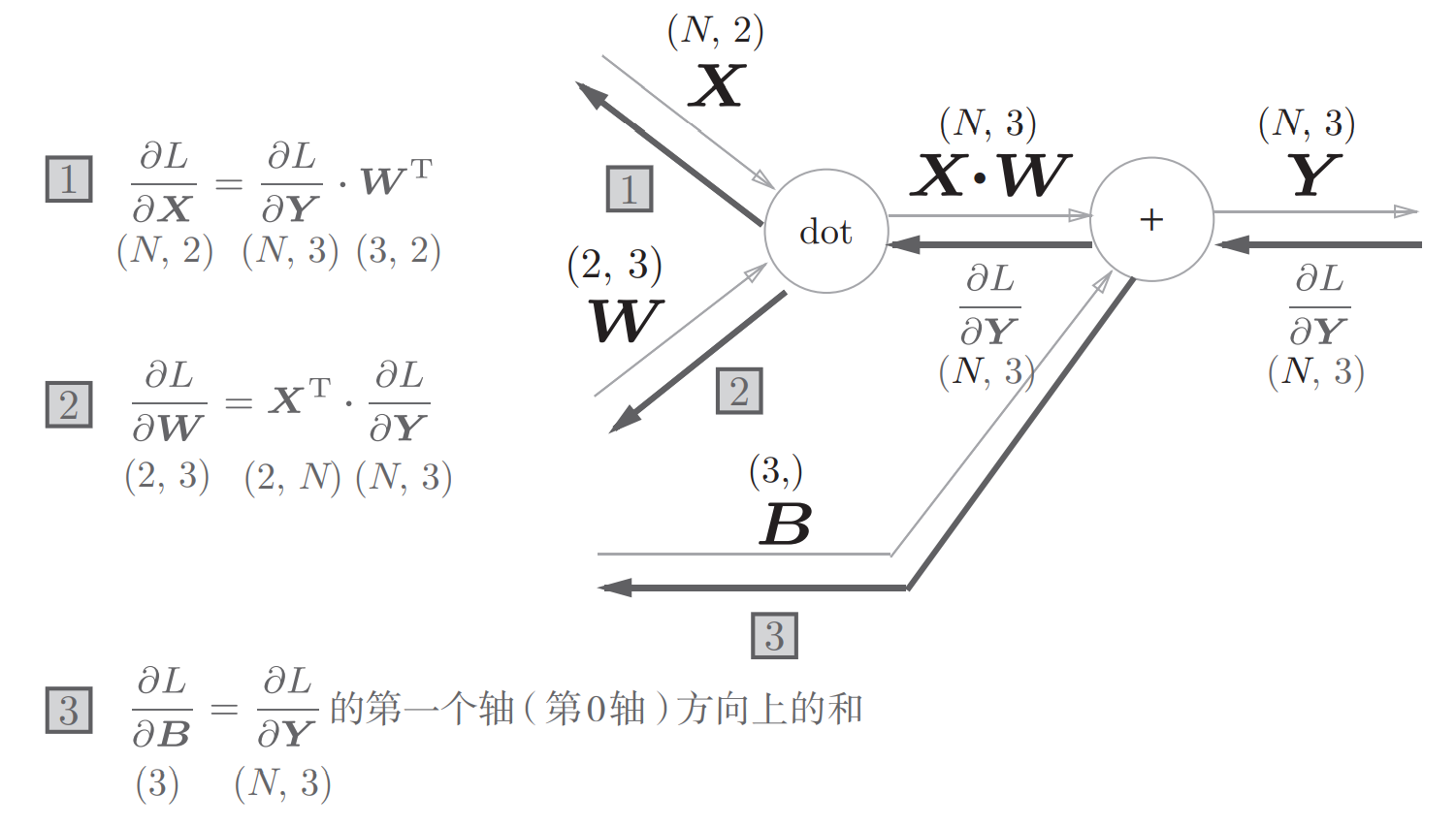

根据计算图用代码来实现一下：

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        return dx

Softmax-With-Loss层

Softmax函数会将输入值正规化之后再输出，比如在一个二分类的神经网络中，最后一层输出的结果为9.1, 0.9，那么softmax函数会将这两个结果进行正规化为0.91, 0,09，即属于第一类的可能是91%，属于第二类的可能是9%。

神经网络中进行的处理有推理和学习两个阶段。神经网络的推理通常不使用 Softmax 层，会将最后一个 Affine 层的输出作为识别结果。神经网络中未被正规化的输出结果有时被称为“得分”。也就是说，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要 Softmax层。不过，神经网络的学习阶段则需要 Softmax 层。

因为要包含损失函数在这一层中，顾称为Softmax-With-Loss层。

以包含交叉熵误差的Softmax-With-Loss层为例，其完整计算图如下：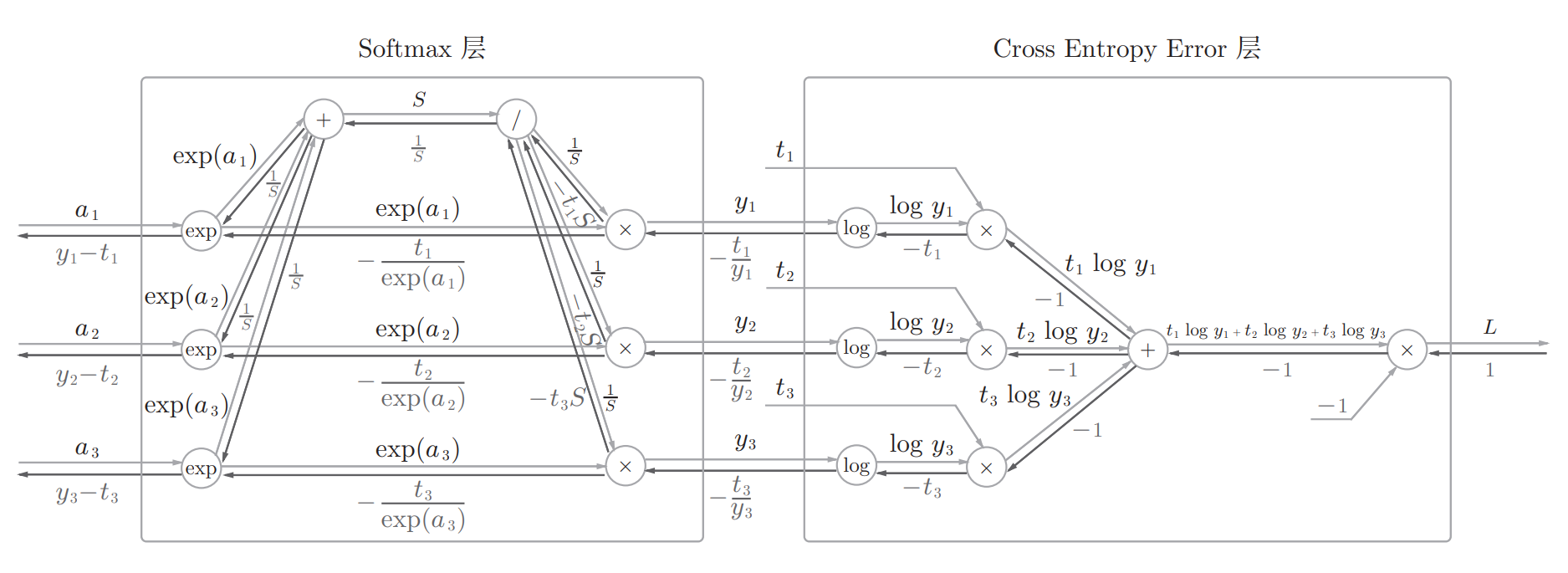

具体实现如下：

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 损失
        self.y = None # softmax的输出
        self.t = None # 监督数据（one-hot vector）

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        return dx

以上就是包含误差反向传播的神经网络各层实现，下一篇文章，我们来实现一下误差反向传播版的手写数字识别，与之前用数值微分实现的方式对比，你会感受到误差反向传播的速度魅力。