在【深度学习笔记】神经网络的学习(3)中,我们使用数值微分的方法去训练神经网络,速度特别慢,这篇文章介绍一下误差反向传播,不再使用数值微分的方法,可以快速计算剃度进行参数的更新。
前置知识
在介绍误差反向传播之前,先来了解一下计算图,计算图可以帮助我们更直观地理解误差反向传播。相比于直接用数学理论证明,计算图对初学者更加友好一些。
依稀记得当时上课老师用数学理论去讲,真是懵逼树上懵逼果,懵逼树下你和我。
计算图
计算图,顾名思义,就是用来表示计算过程的图形,这里说的图形是数据结构中的图,通过多个节点和边表示。光用语言描述不太直观,举个栗子:
法外狂徒张三想去买一个手机,他来到商城,选了一个iPhone 13 Pro,价格标签上写着7072元,下面还有一行小字:需缴纳消费税13.11%。于是张三最后花了7999元买下了这部手机。
这一计算过程用计算图表示如下:
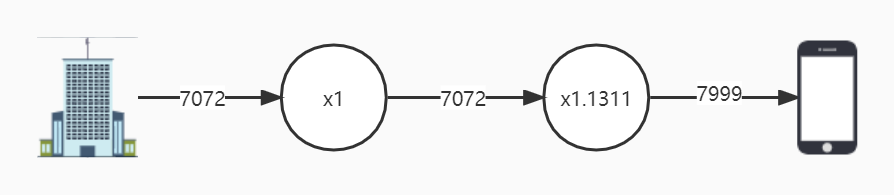
一部手机7022×1=7022元,交税13.11%,最终付款7022×(1+0.1311)=7999元。(所有结果仅保留整数)
再举个栗子,张三买完手机,突然又想买个平板,这次我们画数据流图时,不再将数值写在圆圈里面,把它们写在外面,圆圈里面只写运算符,这样一改,是不是有点前几篇文章中画的神经网络结构图的味道了。
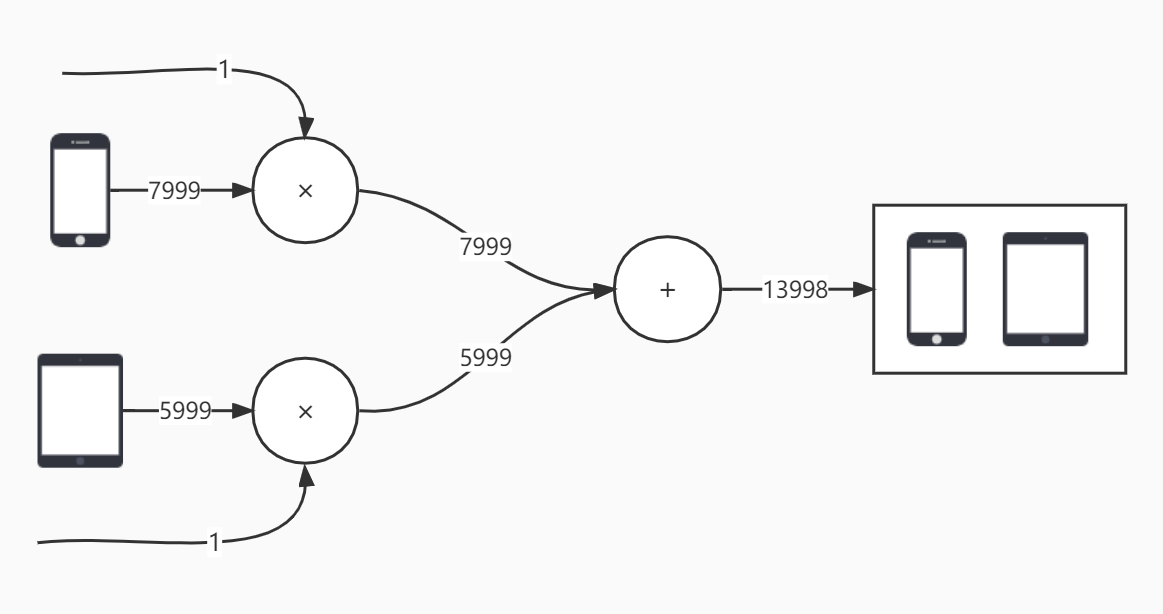
一个手机7999×1=7999元,一个平板5999×1=5999元,总共7999+5999=13998元。
从上面的例子可以看出,计算图的一大优点是将复杂的计算分解成多个简单的“局部计算”,过传递“局部计算”获得最终结果。
计算图可以集中精力于局部计算,无论全局计算多么复杂,各部分只需要进行简单的局部计算,通过传递它的计算结果,便可以获得全局的复杂计算的结果。
计算图这一概念在深度学习框架Tensorflow中有大量运用(数据流图),Tensorflow高效、正确的计算就是通过拓扑排序和计算图保证的。
在了解反向传播之前,还需要一些数学知识:导数、偏导数、链式法则。这里不在赘述,附几篇相关知识的文章:
误差反向传播
上面两个计算图的传播方向都是自左向右,称为正向传播(前馈神经网络),接下来我们看一下自右向左的情况,也就是反向传播(误差反向传播)。
在第一个栗子中,我们计算了张三买1个手机时加上消费税最终需要支付的金额。现在,假设我们想知道手机涨价会多大程度上影响最终的支付金额,即“最终支付金额关于手机的价格的导数”。设手机的价格为$x$,支付金额为$L$,则相当于求$\frac{\partial L}{\partial x}$。这个导数的值表示当手机的价格稍微上涨时,支付金额会增加多少。
反向传播
反向传播的过程如下图,沿着与正方向相反的方向,乘上局部导数。计算顺序是,将信号E乘以节点的局部导数$\frac{d f(x)}{dx}$,然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中$y = f(x)$的导数,也就是$y$关于$x$的导数。
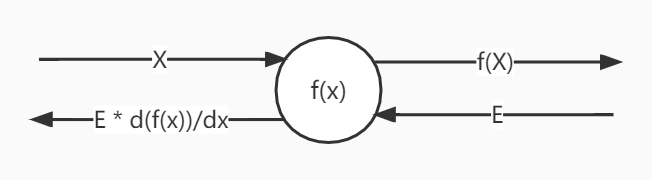
这就是反向传播的计算顺序,可以高效地求出导数的值。
举个详细一点的例子,比如
$$z=(x+y)^2$$
这个算式我们可以拆成$t=x+y$、$z=t^2$这两个小步骤,对他们偏导得:
$$\frac{\partial z}{\partial t}=\frac{\partial t^2}{\partial t}=2t$$
$$\frac{\partial t}{\partial x}=\frac{\partial (x+y)}{\partial y}=1$$
$$\frac{\partial t}{\partial y}=\frac{\partial (x+y)}{\partial y}=1$$
根据复合函数求导的链式法则,就有:
$$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial t} \frac{\partial t}{\partial x}=2t=2(x+y)$$
画成计算图就是: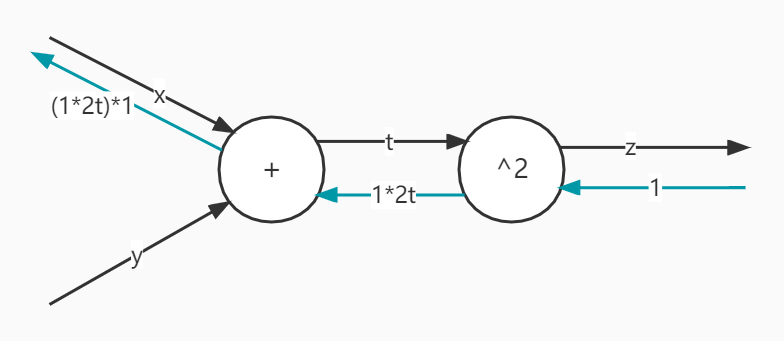
看到这里,相信上面举的两个栗子你也可以画出反向传播的计算图了,不妨拿起笔画一画试试。
有关计算图解释反向传播的更多内容,可以查看这篇博客:Hacker's guide to Neural Networks
到这里,有关误差反向传播的理论准备就差不多了,下一篇我们来实现一下误差反向传播。

Comments | NOTHING