之前一致没看严奶奶《数据结构》这本书上的排序这一部分，今天看了一下这一章的内容，里面的快速排序一上来的我看蒙了，怎么和我之前学的快速排序不一样？？？
为了弄清楚到底哪个是快排的标准写法，我“考古”了一下C. A. R. Hoare大佬1960年快排的论文，发现和我学会的快排又不一样（我是看《算法》这本书学的快排），三个版本的快排。
这一下子兴趣就起来了，这三个到底有啥区别。（突然想到《孔乙己》，“茴字有四样写法，你知道么？”，快排有三种写法（好像不止三种），你知道么？）
下面我先写一下三个快排的大体思想。

论文原版快排

论文原文下载地址：点击下载
找一个“标兵”$bound$（如第一个元素），两个指针，一个$i$，指向数组开始，一个$j$，指向数组最后一个元素，$i$先动，从左边找一个小于$bound$的值，然后$j$再动，找一个大于$bound$的值，然后交换两个指针指向的元素，如此反复，直到$i$和$j$两个指针“擦肩而过”，“标兵归位”（标兵与当前$j$指向的元素交换），至此，结束一轮，再递归对两边执行该操作。

严奶奶版快排（建议考研参考此方法）

找一个“标兵”$p$（第一个元素），两个指针，一个$i$，指向数组开始，一个$j$，指向数组最后一个元素，$j$先动，从右边开始找一个大于$p$的值，直接赋值给当前$i$指向的元素（因为$i$指向的元素已经复制给$p$临时保存，所以不会丢失），然后$i$再动，从左边找一个小于$p$的值，直接赋值给当前$j$指向的元素（刚刚这个值已经赋给了，之前$i$指向的位置，所以当前$j$指向的值也不会丢失），如此反复，直到$i >= j$时，将$p$赋值给当前$i$指针指向的位置，至此，结束一轮，再递归对两边执行该操作。

算法(第四版)中的快排（网络上广为流传的版本）

找一个“标兵”$v$（第一个元素），两个指针，一个$i$，指向数组开始，一个$j$，指向数组最后一个元素，$j$先动，从右边开始找一个大于$v$的值，然后$i$再动，从左边开始找一个小于$v$的值，然后交换两个指针指向的元素，如此反复，直到$i >= j$时，将$v$和当前$j$指针指向的元素交换，至此，结束一轮，再递归对两边执行该操作。

三种对比

论文原版是左指针先动，右指针再动，严奶奶和《算法》这本书中的是右指针先动，左指针再动。手动模拟一趟排序过程可以发现，论文原版和《算法》中的中间结果一样，严奶奶的与这两个不同。一般在考试中，排序考的就是中间结果，国内大学又多以严奶奶的书为教材或参考书，所以在期末或者考研中建议还是按严奶奶的方法来（或者其他指定的参考书）。想想之前我数据结构这门课的实际分数和我预期分数的差异，好像知到是因为哪里写错了。

此处应该有模拟一趟排序的图，但博主太懒还没画，先占个空，可以自己随便写个数组画画哈，不想画还急着看文末评论踢我一下。

性能对比

从理论分析上来看，最好情况都是$O(NlogN)$，最坏情况都是$O(N^2)$，但时从算法思路和手动模拟过程，就能看出来，原版会发生两个指针“擦肩而过”，会进行不必要的遍历，所以性能应该会低一些。下面直接从实际对比三种快排算法。
使用随机数函数生成$10^6$个数据，然后排序测试，结果如下：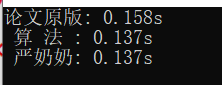

意料之中，论文原版性能最差，严奶奶的和《算法》中的五五开。

当数据量达到$10^7$时候，结果如下：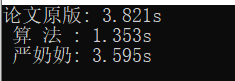

《算法》中的快排比另外两个快了一半！

测试代码(一开始只是打算测试看看，解答自己的疑惑，所以命名比较随意，勿喷)：

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
// 内联函数，要多次交换元素，调用次数多，防止函数调用开销影响最后结果
inline void swap(int* x, int* y) {
    int temp = *x;
    *x = *y;
    *y = temp;
}

//////////// 严奶奶版本开始  /////////// 
int partitionYan(int* arr, int low, int high) {
    int p = arr[low];
    while(low < high) {
        while(low < high && arr[high] >= p)
            high--;
        arr[low] = arr[high];
        while(low < high && arr[low] <= p)
            low++;
        arr[high] = arr[low];
    }
    
    arr[low] = p;
    
    return low;
} 

void QuickSortYan(int* A, int low, int high) {
    int q;
    if(low < high)
    {
        q = partitionYan(A, low, high);
        QuickSortYan(A, low, q-1);
        QuickSortYan(A, q+1, high);
    }
}
//////////// 严奶奶版本结束  /////////// 

//////////// 论文原版开始  /////////// 
int Partition(int* A, int low, int high) {
    int i = low, j = high;
    // choos a bound
    int bound = A[low];
    
    while(1) {
        // lower pointer start first, when the item equal to or less than bound, move upper
        while(A[i] <= bound && i<=j) i++;
        // then upper pointer start, when the ietm equal to or greater than bound, move lower
        while(A[j] >= bound && i<=j) j--;
        
        // The process continues until the pointers cross each other
        if(i >= j)
            break;
        // exchange 
        swap(&A[i], &A[j]);
    }
    
    // The aim is now to produce a situation in 
    // which the keys of all items below a certain dividing line are equal to or less than the bound,
    // while the keys of all items above the dividing line are equal to or greater than the bound.
    // 所有元素交换完成后，要将 bound 放到两个 子数组的中间，以满足上述要求
    A[low] = A[j];
    A[j] = bound;
    
    return j;
}

void QuickSort(int* A, int low, int high) {
    int q;
    if(low < high)
    {
        q = Partition(A, low, high);
        QuickSort(A, low, q-1);
        QuickSort(A, q+1, high);
    }
}
//////////// 论文原版结束  /////////// 

//////////// 《算法》版本开始 /////////// 
int partition(int* a, int lo, int hi) {
    int i = lo, j = hi + 1;
    int v = a[lo];
    while(true) {
        while(a[++i] < v)
            if(i == hi)
                break;
        while(a[--j] > v)
            if( j == lo)
                break;
                
        if(i >= j) break;
        swap(a[i], a[j]);
    }
    swap(a[lo], a[j]);
    return j;
}

void QuickSortA(int* A, int low, int high) {
    int q;
    if(low < high)
    {
        q = partition(A, low, high);
        QuickSortA(A, low, q-1);
        QuickSortA(A, q+1, high);
    }
}
//////////// 《算法》版本结束 /////////// 


int main() {
    clock_t start, end;
    unsigned seed;
    seed = time(0);
    srand(seed);
    
    int size = 1e7;
    
    int* data1 = new int[size];
    int* data2 = new int[size];
    int* data3 = new int[size];
    // 制造数据 
    for(int i = 0; i < size; i++) {
        data1[i] = rand();
        data2[i] = data1[i];
        data3[i] = data1[i];
    }
    // QuickSort：论文原版 
    // QuickSortA：  算法第四版
    // QuickSortYan： 严奶奶版 
    start = clock();
    QuickSort(data1, 0, size-1);
    end = clock();
    cout<< "论文原版: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;
    
    start = clock();
    QuickSortA(data3, 0, size-1);
    end = clock();
    cout<< " 算 法 : " << (double)(end - start) / CLOCKS_PER_SEC<< "s" << endl;
    
    start = clock();
    QuickSortYan(data2, 0, size-1);
    end = clock();
    cout<< " 严奶奶: " << (double)(end - start) / CLOCKS_PER_SEC<< "s" << endl;
    
    return 0;
}