【深度学习笔记】优化算法

上篇文章，我们实现了一个三层神经网络，并训练了一个识别手写数字的模型。
神经网络的训练过程，就像是一个炼丹的过程，炼丹师拿来药材（数据），支起八卦炉（模型），生起六昧真火（优化算法），然后静静等待丹药（模型）出炉。丹药炼的好不好，除了和药材、炉子有关，和火候也有脱不了的关系。

在前面几篇文章，我们使用的火是SGD，SGD也是最简单的一个优化算法。也就是说SGD是最初级的炉火，那么可想而知，在炼一些对温度要求较高的丹药时，SGD可能就火力不够了。

举个栗子，比如函数：

$$ f(x,y)=\frac{1}{20}x^2+y^2 $$

画个图像来看一看：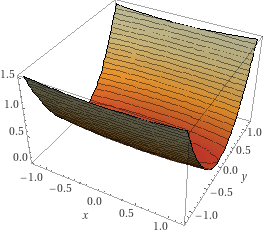

长得像个排水沟一样，那么如果我们从$z$轴正方向向下看（只看$x$、$y$轴）又是啥样呢？如下图：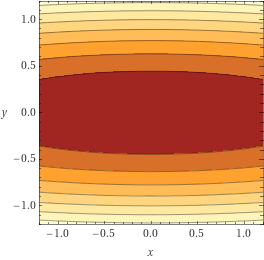

两张图片结合起来看，真的很像个排水沟，或者说是河道。我们来看一下这个函数的梯度，这个梯度的特征是，$y$轴方向上大，$x$轴方向上小，就是$y$轴方向的坡度大，而$x$轴方向的坡度小。从图片可以明显看出，函数的梯度是从两边指向$$y=0$$的，很多地方的梯度没有指向最小值点$(0, 0)$。我们再回顾一下SGD的更新策略：

$$ W = W - \eta \frac{\partial L}{\partial W} $$

其中$W$表示要更新的权重参数，$\eta$是学习率，$\frac{\partial L}{\partial W}$为损失函数对权重的梯度。
即SGD只会像梯度方向前进，如果使用SGD对上面这个函数求最优解（求最小值），由于多处梯度没有指向最优解点，所以求解过程是一个漫长曲折的过程，相当低效。看一下SGD的搜索路径，呈“之”字型：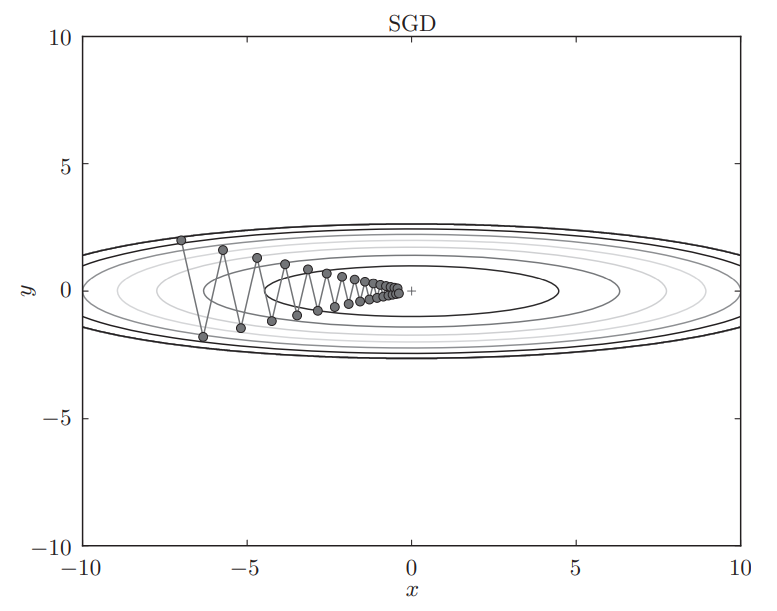

这就看出了SGD的缺点：如果函数的形状非均向，比如呈延伸状，搜索的路径就会非常低效。可能会在沟壑两边震荡，停留在局部最优点。

下面我们来学习几个改进之后的优化算法，以便在炼丹的时候可以针对不同丹药调节火力。

Momentum 算法

又称SGDM算法（SGD with Momentum），这是为了抑制SGD震荡而提出的，其表达式如下：

$$ v=\alpha v - \eta \frac{\partial L}{\partial W} $$

$$ W = W + v $$

其中$W$，$\eta$，$\frac{\partial L}{\partial W}$与SGD中含义相同，新出现的变量$v$，其物理含义是速度。可以理解为是SGD中加入了重力对下坡速度的影响，SGD下坡时以匀速前进，引入$v$后，下坡时陡坡走的快，缓坡走的慢。
代码实现:

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

            for key in params.keys():
                self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
                params[key] += self.v[key]

AdaGrad 算法

在【深度学习笔记】神经网络的学习(2)中，我们介绍过学习率对学习过程的影响：学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。
那我们了能不能动态调整学习率，一开始学习率大，让参数快速更新，慢慢减小学习率，防止模型发散呢？AdaGrad 正是这样一个学习率衰减的算法。其数学表达式为：

$$ h=h+\frac{\partial L}{\partial W} \bigodot \frac{\partial L}{\partial W} $$

$$ W = W - \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial W} $$

其中$\bigodot$对应矩阵元素的乘法，通过乘$\frac{1}{\sqrt{h}}$对学习率进行约束。

代码实现：

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

Adam 算法

Adam算法可以看作是 Momentum 和 AdaGrad 的结合体，既可以根据坡的陡缓来调节速度，又根据训练时间来调节速度，拥有两者的共同优点。还有结合了 Nesterov 的 Nadam 算法，拥有 Momentum、AdaGrad、Nesterov 的优点，看似完美的Adam/Nadam，其实并不是特别完美。

Adam 两宗罪

看到这里，是不是感觉SGD弱爆了，只会无脑沿梯度更新。SGD高呼：冤枉啊。
举个栗子，现在相机都带有一个自动模式，可以自动根据环境来调节ISO、光圈、快门速度，可以拍出一张还不错的照片，但为何相机都还保留了手动调节参数的功能呢？因为要想拍一张完美精细的照片，可能自动调节的参数并不是特别合适，需要摄影师手动调节。（也或许是为了方便摄影师装X？[手动狗头]）

上等的食材要用最原始的烹饪方式，机器学习也一样，有时候需要我们用最原始的方法做精准的调优。

Adam 看似是一个集大成之作，但它有两个致命的弱点，下面我们来谈谈：

模型可能不收敛

在论文 On the Convergence of Adam and Beyond 中用反例证明了在一些情况下，模型可能不收敛。

可能错过全局最优解

深度学习参数众多，在一个维度极高的空间中，目标函数起起伏伏，拥有无数个高峰和洼地，引入动量后可能导致错过全局最优解。比如论文 The Marginal Value of Adaptive Gradient Methods in Machine Learning 中提到的情况，用自适应算法求出的答案非常差。
又比如在 Improving Generalization Performance by Switching from Adam to SGD 中提到，使用 Adam 的收敛速度比 SGD 快，但最终效果是 SGD 比较好。

那么我们该怎么选择炼丹用的火呢，下篇文章我们再来谈谈。